Bismillah Alhamdulillah,

Dalam artikel ini akan dibahas bagaimana cara mendapatkan faktorisasi atau penguraian bilangan prima dari sebuah bilangan.

1. Pendahuluan

Faktor adalah pembagi suatu bilangan yang dapat membagi habis bilangan tersebut. Kalau saya punya sebuah angka 6, maka faktor bilangannya adalah: 1, 2, 3, 6. Yaitu hasil perkalian dari:

1 x 6
2 x 3

Berikutnya, kita membahas pengertian faktorisasi dan faktorisasi prima.

Faktorisasi dalam matematika adalah dekomposisi suatu objek (misalnya, suatu bilangan, polinomial, atau matriks) menjadi suatu produk objek lain, atau faktor, yang ketika dikalikan bersama menghasilkan bilangan asalnya. Contohnya, bilangan 15 difaktorkan menjadi bilangan prima sebagai 3 × 5, dan polinomial x2 − 4 difaktorkan menjadi (x − 2)(x + 2). Dalam segala kasus, diperoleh suatu produk dari objek yang lebih sederhana - Wikipedia .

Faktorisasi prima adalah pecahan bilangan komposit yang terdiri dari bilangan-bilangan pembagi yang lebih kecil, dan hasil perkalian dari bilangan-bilangan tersebut sama dengan bilangan komposit yang disebutkan. Contohnya, faktorisasi prima bilangan 84 adalah 2x2x3x7, di mana bilangan 2, 3 dan 7 adalah bilangan prima dan bilangan pembagi 84 - Wikipedia.

---

2. Pembahasan

Dalam bagian pembahasan ini akan saya jabarkan langkah per langkah cara membangkitkan faktor bilangan menggunakan bahasa pemrograman Python.

a. Faktor bilangan

Pertama-tama, kita akan tampilkan sisa hasil pembagian dari sebuah bilangan dengan angka 1 s/d bilangan itu sendiri.

angka = 6
for i in range(1, angka + 1):
    print(f"{angka} % {i} = {angka%i}")

Luaran dari kode tersebut di atas adalah:

6 % 1 = 0
6 % 2 = 0
6 % 3 = 0
6 % 4 = 2
6 % 5 = 1
6 % 6 = 0

Dari sini kita dapat modifikasi kode untuk dapat menampilkan bilangan yang sisa hasil baginya nol saja.

angka = 6
for i in range(1, angka + 1):
    if angka % i == 0:
        print(i, end=" ")

# luaran = 1 2 3 6

Bahkan dapat kita kompres lagi kodenya dan memasukkan datanya ke dalam sebuah list.

faktor = [i for i in range(1,angka+1) if angka%i==0]
print(faktor)

# luaran = [1, 2, 3, 6]

b. Hasil perkalian

Berikutnya, kita akan mencoba menampilkan detail hasil perkalian dari faktor bilangan yang diperoleh. Hasil perkalian dalam faktor bilangan melibatkan minimal 2 angka. Sebelum membahas lebih lanjut ke menampilkan hasil perkalian, berikut ini contoh faktor bilangan pada beberapa angka.

6 = [1, 2, 3, 6] ➡️ 4 angka
20 = [1, 2, 4, 5, 10, 20] ➡️ 6 angka
100 = [1, 2, 4, 5, 10, 20, 25, 50, 100] ➡️ 9 angka

Cara menemukan hasil perkalian yang paling mudah dapat dilihat pada ilustrasi berikut.

Kodenya adalah sebagai berikut.

angka = 6
listOutput = []
faktor = [i for i in range(1,angka+1) if angka%i==0]
jml = len(faktor)//2 + len(faktor)%2
for i, data in enumerate(faktor):
    if i==jml: break
    listOutput.append((faktor[i], faktor[-1-i]))

print(listOutput)

Kalau variabel angka diisi dengan angka 6 dan 100 secara bergantian, maka luarannya adalah:

# angka = 6
[(1, 6), (2, 3)]

# angka = 100
[(1, 100), (2, 50), (4, 25), (5, 20), (10, 10)]

Untuk kemudahan pemanfaatan fungsional pembangkitan faktor bilangan dan menampilkan hasil perkalian, kode di atas dapat kita buat dalam bentuk fungsi.

def faktor_bilangan(angka):
    listOutput = []
    faktor = [i for i in range(1,angka+1) if angka%i==0]
    jml = len(faktor)//2 + len(faktor)%2
    for i, data in enumerate(faktor):
        if i==jml: break
        listOutput.append((faktor[i], faktor[-1-i]))
    return faktor, listOutput

angka = 100
bilFaktor, hasilKali =  faktor_bilangan(angka)
print(f"Bilangan faktor dari {angka} adalah {bilFaktor}")
print(f"Hasil perkalian = {hasilKali}")

Contoh luarannya adalah:

Bilangan faktor dari 100 adalah [1, 2, 4, 5, 10, 20, 25, 50, 100]
Hasil perkalian = [(1, 100), (2, 50), (4, 25), (5, 20), (10, 10)]

c. Pemeriksaan akar kuadrat

Untuk membantu mempercepat penemuan faktor bilangan prima, kita harus memeriksa apakah bilangan yang ada dalam list faktor bilangan memilik akar kuadrat atau tidak.

Misalkan kita punya angka 100, memiliki faktor bilangan 1, 2, 4, 5, 10, 20, 25, 50, 100. Dari daftar faktor bilangan tersebut, kita dapat memeriksa apakah bilangan di dalamnya ada yang memiliki akar kuadrat atau tidak. Berikut ini kodenya.

import math
def punya_akar_kuadrat(angka):
    akar = math.sqrt(angka)
    kuadrat = (int(akar+0.5) ** 2 == angka)
    return kuadrat

angka = 9
print(punya_akar_kuadrat(angka))
# angka 9 -> luaran = True
# angka 10 -> luaran = False

Untuk keperluan faktorisasi prima, fungsi akar kuadrat dimodifikasi sedemikian rupa agar dapat menampilkan nilai akarnya jika bilangan tersebut memiliki akar kuadrat. Sebaliknya, akan mengembalikan nilai None. Kode adalah sebagai berikut.

def akar_kuadrat(angka):
    akar = math.sqrt(angka)
    if int(akar+0.5) ** 2 == angka:
        return int(akar)
    else:
        return None

d. Faktorisasi prima

Alur proses dari faktorisasi prima adalah sebagai berikut.

• Masukkan angka ke list penampung, tetapkan list indeks ke nol sebagai angka masukan;
• Cari akar kuadrat dari angka masukan jika ditemukan, kemudian dua akar diletakkan dalam sebuah list penampung. Misal angka masukan adalah 9, maka isi list penampung adalah [3, 3]. Kemudian, hapus data angka masukan yang pertama tadi dari list penampung. Jika tidak ditemukan akar kuadratnya, menuju langkah berikutnya;
• Bangkitkan faktor bilangan dari angka masukan, periksa jumlah bilangan yang ada di dalamnya. Jika jumlah bilangan ada 2, berarti angka tersebut merupakan bilangan prima. Misalnya, angka 2 memiliki faktor bilangan [1, 2], angka 3 memiliki faktor bilangan [1, 3], dan seterusnya sesuai definisi bilangan prima. Angka tersebut selanjutnya ditambahkan ke list luaran akhir.
• Jika jumlah bilangan lebih dari 2 -- yang tidak termasuk dalam bilangan prima -- maka, list faktor bilangan sepenuhnya ditambahkan ke list penampung dan hapus data angka masukan dari list penampung.
• Langkah-langkah ini diulangi terus hingga list penampung kosong.
• Luaran akhir akan berisi daftar hasil faktorisasi bilangan prima.

Berikut ini kodenya.

def faktorisasi_prima(angka):
    lstFaktorisasiPrima = []
    lstTemp = [angka]

    while True:
        angka = lstTemp[0]
        akar = akar_kuadrat(angka)
        if akar:
            lstTemp.remove(angka)
            lstTemp.extend([akar, akar])
        else:
            _, lstFaktor = faktor_bilangan(angka)
            if len(lstFaktor)>1:
                lstTemp.remove(angka)
                lstTemp.extend(lstFaktor[1])
            else: # prima
                lstTemp.remove(angka)
                lstFaktorisasiPrima.append(angka)

        if not lstTemp: break
    return lstFaktorisasiPrima

Berikut ini contoh hasil faktorisasi bilangan prima dengan angka masukan yang berbeda-beda.

6 ➡️ [2, 3]
50 ➡️ [2, 5, 5]
84 ➡️ [2, 2, 3, 7]
100 ➡️ [2, 5, 2, 5]
1224 ➡️ [2, 2, 2, 3, 3, 17]

e. Penyederhanaan hasil faktorisasi prima

Inti dari faktorisasi prima sebenarnya sudah selesai, tinggal menyederhanakan tampilan dengan menggunakan tanda pangkat pada bilangan yang sama berulang lebih dari satu kali. Misalnya, angka masukan 1224, yang memiliki bilangan faktor prima [2, 2, 2, 3, 3, 17]; bentuk sederhananya adalah 2^3 x 3^2 x 17^1 atau 2³ x 3² x 17¹. Kodenya adalah sebagai berikut.

def kamus_penyederhanaan(listFaktorPrima):
    kamus = Counter(listFaktorPrima)
    lst = []
    for i in kamus:
        lst.append(f"{i}^{kamus[i]}")
    return lst

Dari hasil penggabungan fungsi-fungsi yang sudah dibuat sebelumnya, kode pemanggilannya adalah sebagai berikut.

angka = 100
hasil = faktorisasi_prima(angka) 

print(f"Hasil faktorisasi prima dari angka {angka} adalah {hasil}")

strSederhana = " x ".join(kamus_penyederhanaan(hasil))
print(f"Bentuk sederhana: {strSederhana}")

Contoh luarannya adalah:

Hasil faktorisasi prima dari angka 100 adalah [2, 5, 2, 5]
Bentuk sederhana: 2^2 x 5^2

f. Versi penelusuran pohon faktor - rekursif

Untuk menentukan faktorisasi prima dari suatu bilangan, kita juga dapat menggunakan sebuah alat bantu bernama pohon faktor. Mekanismenya adalah dengan membagi bilangan tersebut berturut-turut dengan bilangan prima dari yang paling kecil terlebih dahulu. Ilustrasi penelusuran pencarian faktor bilangan prima dari angka 100 dapat dilihat pada gambar berikut.

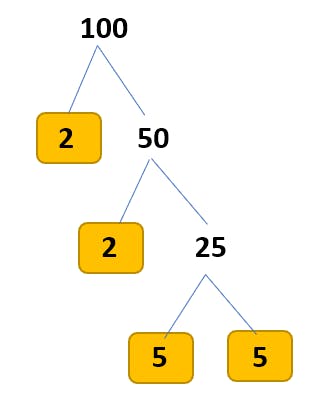
Alur prosesnya adalah:

• Cari bilangan faktor terkecil dari angka masukan.
• Temukan pengalinya, yang mana pengali adalah hasil pembagian antara angka masukan dan bilangan faktor pembagi.
• Langkah-langkah ini diulang terus menerus hingga ditemukan pengali yang termasuk dalam bilangan prima. Hal ini berarti faktor bilangan terkecilnya adalah dirinya sendiri.

Urutan proses penguraiannya adalah sebagai berikut.

🟢MULAI 🟢
✅angka = 100
➜ faktor bilangan terkecil = 2
➜ pengali = 50
✅angka = 50
➜ faktor bilangan terkecil = 2
➜ pengali = 25
✅angka = 25
➜ faktor bilangan terkecil = 5
➜ pengali = 5
🔴STOP🔴
➜ Kumpulkan semua bilangan terkecil sebelumnya ditambah pengali paling akhir.
☑️Luaran = [2, 2, 5, 5]

Fungsi rekursif diterapkan pada tahapan pencarian faktor bilangan prima terkecil. Kode lengkapnya adalah sebagai berikut.

def faktor_prima_rekursif(angka, lst=[]):
    # jika list kosong
    if not lst:
        if angka == 1:
            return [angka]
        elif angka < 1:
            return None

    # pembagi adalah faktor bilangan terkecil di atas angka 1
    pembagi = next(i for i in range(2, angka+1) if angka % i == 0)

    if angka == pembagi:
        lst.append(angka)
        return lst

    pengali = angka // pembagi
    print(f"Perkalian tingkat {len(lst) + 1} = {pembagi} x {pengali}")

    if pembagi != pengali:
        lst.append(pembagi)
        return faktor_prima_rekursif(pengali)
    else:
        lst.extend([pembagi, pengali])
        return lst

Contoh luarannya (dengan ditambah pemrosesan ke bentuk sederhana seperti di bagian sebelumnya) adalah:

Perkalian tingkat 1 = 2 x 50
Perkalian tingkat 2 = 2 x 25
Perkalian tingkat 3 = 5 x 5
Hasil: [2, 2, 5, 5]
Bentuk sederhana: 2^2 x 5^2

---

3. Penutup

Dalam bidang ilmu Matematika, bilangan prima erat kaitannya dengan tingkat pembelajaran yang lebih tinggi, seperti mencari faktor persekutuan terbesar (FPB), menyederhanakan pecahan, dan lain-lain. Bilangan prima juga digunakan dalam ilmu kriptografi untuk melakukan enkripsi atau penyamaran data. Penerapan konsep ini memegang peranan penting dalam keamanan data, misalnya keamanan akun untuk login sistem, keamanan jaringan komputer, sistem keamanan bidang perbankan, dan lain sebagainya.

Semoga bermanfaat.

Terima kasih.

---

Cek repositori di tautan berikut atau cek demo secara daring .

---

Catatan revisi tulisan.

✏️[2-12-2021]
Penambahan tulisan metode penelusuran pohon faktor - rekursif.

✏️[1-12-2021]
Metode alternatif yang sebelumnya ditulis ternyata mengandung bugs. Hal ini menyebabkan kesalahan hitungan pada angka masukan berukuran besar. Sementara saya hapus dahulu.