Search for a command to run...
Tutorial menyelesaikan persoalan menghitung jumlah terjadinya jabat tangan (salaman) dalam sejumlah orang menggunakan Python dengan 5 metode berbeda.
Lecturer & Researcher at Informatics Engineering. Universitas Komputer Indonesia. Bandung
No comments yet. Be the first to comment.
Bismillah walhamdulillah. Bagaimana memanfaatkan library google.colab.ai untuk tanya jawab, Text2SQL, NER, analisis sentimen, hingga penilaian jawaban — langsung dari Colab, bahkan untuk pengguna gratis. Pendahuluan Model bahasa generatif seperti Gem...
Langkah-Langkah Praktis untuk Membuat Dialog Interaktif Menggunakan Google Gemini API dengan Python.
JSON adalah format data yang ringan dan populer untuk pertukaran data antar aplikasi. Artikel ini membahas pengelolaan JSON menggunakan Python.
Modul PIL atau Pillow banyak digunakan untuk keperluan pengolahan citra. Dalam artikel ini akan dibahas beberapa fitur dasar penggunaannya.
Para ulama berkata, "Dalam menafsirkan Al Quran diperlukan keahlian dalam lima belas bidang ilmu." Dalam artikel ini akan dituliskan ringkasannya.
Bismillaah Alhamdulillah,
Pada suatu waktu, saya melihat contoh soal pelajaran Matematika di internet seperti ini:
Di dalam sebuah ruangan terdapat 46 orang yang mengadakan sebuah kegiatan, selesai kegiatan mereka saling berjabat tangan. Berapa kalikah terjadi jabat tangan atau bersalaman di antara keduanya tanpa pernah bersalaman 2 kali pada orang yang sama?
Model soal seperti ini sering dibahas penyelesaiannya menggunakan teori penyelesaian barisan bilangan (barisan aritmetika) dan kombinasi. Merupakan bagian dari pelajaran Matematika di kelas 7-8 (SMP) dan/atau di tingkat SMA untuk tingkat lanjut.
Dalam artikel ini akan saya bahas penyelesaiannya menggunakan bahasa pemrograman Python melalui 5 metode berbeda, yaitu (1) iterative, (2) recursive, (3) barisan aritmetika, (4) deret aritmetika, dan (5) kombinasi.
Jabat tangan dapat terjadi minimal oleh 2 orang, serta cukup dilakukan 1 kali saja. Jika dimisalkan terdapat dua orang A dan B, maka jabat tangan dapat disimbolkan dengan A-B. Dan tidak perlu disimbolkan sebaliknya, seperti B-A, karena hal ini sudah diwakili oleh A-B. Dan jika terdapat 3 orang A,B, dan C (disingkat ABC), maka jabat tangan yang terjadi sebanyak 3 kali, yaitu A-B (A dengan B), A-C (A dengan C), dan B-C (B dengan C). Bagaimana kalau 4 orang? Maka, jabat tangan yang terjadi adalah A-B, A-C, A-D, B-C, B-D, dan C-D; dengan total sebanyak 6 kali.
Jadi, kalau kita ringkas jumlah orang dan jabat tangan yang terjadi adalah sebagai berikut.
| Jumlah orang | Simbol | Jabat tangan | Jumlah |
| 2 | AB | A-B | 1 |
| 3 | ABC | A-B, A-C, B-C | 3 |
| 4 | ABCD | A-B, A-C, A-D, B-C, B-D, C-D | 6 |
| 5 | ABCDE | A-B, A-C, A-D, A-E, B-C, B-D, B-E, C-D, C-E, D-E | 10 |
Penerapan dalam pemrograman mengikuti simulasi pada gambar berikut.
Dalam gambar tersebut di atas menyimulasikan relasi terjadinya jabat tangan dalam 2, 3, dan 4 orang. Kode utamanya adalah seperti ini.
jml_orang = 4
jml_salaman = 0
for i in range(1, jml_orang):
for j in range(i + 1, jml_orang + 1):
jml_salaman += 1
print(i,j)
print(jml_salaman)
Pasangan jabat tangan adalah 1 2, 1 3, 1 4, 2 3, 2 4, 3 4 dan isi jumlah salaman adalah 6. Adapun dalam kode berikut dimodifikasi sedemikian rupa agar tampilan jabat tangan sesuai dengan rencana awal, yaitu simbol huruf abjad A, B, C, dan seterusnya.
# inisialisasi jumlah orang
jml_orang = 4
# inisialisasi simbol orang
simbol_A = 65 # karakter ASCII A:65, Z:91
simbol_akhir = simbol_A+jml_orang-1
# jumlah orang harus lebih dari 1 dan kurang dari 27 (simbol A-Z)
assert 1 < jml_orang < 27
# penampung jumlah salaman, inisialisasi 0
jml_salaman = 0
for i in range(simbol_A, simbol_akhir):
for j in range(i + 1, simbol_akhir + 1):
jml_salaman += 1
print(f"{chr(i)}-{chr(j)}")
print(f"\nJumlah salaman yang terjadi dalam {jml_orang} orang = {jml_salaman} kali")
Luarannya adalah:
A-B
A-C
A-D
B-C
B-D
C-DJumlah salaman yang terjadi dalam 4 orang = 6 kali
Berikutnya kita coba bahas penyelesaian persoalan jumlah jabat tangan (salaman) ini melalui metode yang berbeda-beda.
Terdapat 5 metode yang akan dibahas dalam hal ini, meliputi: (1) iterative, (2) recursive, (3) barisan aritmetika, (4) deret aritmetika, dan (5) kombinasi. Beberapa metode akan disampaikan teori dasar yang digunakan, dan kemudian ditambahkan contoh kode yang dapat digunakan.
Metode iterative ini sebenarnya hanya memanfaatkan perulangan (atau iterasi) seperti biasa. Skema perulangan mengacu pada mekanisme penjumlahan data seperti terlihat pada tabel berikut.
| Jumlah orang | Cara menjumlahkan | Jumlah jabat tangan |
| 2 | tidak ada penjumlahan | 1 |
| 3 | 1 + 2 | 3 |
| 4 | 1 + 2 + 3 | 6 |
| 5 | 1 + 2 + 3 + 4 | 10 |
Kodenya adalah sebagai berikut.
def Hitung_Jumlah_Salaman(jml_orang):
total = 0
for i in range(1, jml_orang):
total += i
return total
Kode tersebut dapat diringkas lagi dengan meniadakan perulangan, yaitu memanfaatkan fungsi bawaan sum untuk menghitung total nilai dari sekumpulan data nilai. Sehingga, hasil akhirnya cukup total = sum(range(1, jml_orang)) dengan menghilangkan inisiasi peubah total dan perulangan.
Dalam metode recursive atau rekursif ini, kita dapat membuat fungsi yang dapat memanggil dirinya sendiri. Hal ini dapat menyederhanakan kode, walaupun akan memakan memori lebih besar untuk pemrosesan data yang besar 1 .
Mari kita anggap bahwa terdapat sebuah fungsi F(x) yang menerima data (parameter) masukan berupa x, yaitu jumlah orang. Jika jumlah orang diisi dengan angka 2 atau F(2), maka luaran jumlah jabat tangan adalah 1. Jika diisi 3 atau F(3), luarannya 3, dan seterusnya. Selanjutnya, mari kita periksa pola penghitungannya dalam tabel berikut.
| Jumlah orang | Fungsi rekursif | Penjumlahan | Jumlah jabat tangan |
| 2 | F(2) | tidak ada penjumlahan | 1 |
| 3 | F(3) | F(2) + 2 = 1 + 2 | 3 |
| 4 | F(4) | F(3) + 3 = 3 + 3 | 6 |
| 5 | F(5) | F(4) + 4 = 6 + 4 | 10 |
| ... |
Dari pola tersebut, kita mengetahui bahwa dengan jumlah orang sebanyak x , maka rumusnya adalah F(x) = F(x-1) + (x-1). Berikut ini kodenya.
def Rekursif_Jumlah_Salaman(jml_orang):
if jml_orang == 2:
return 1
else:
return Rekursif_Jumlah_Salaman(jml_orang - 1) + (jml_orang - 1)
Mekanisme kerjanya dapat dilihat pada gambar berikut.
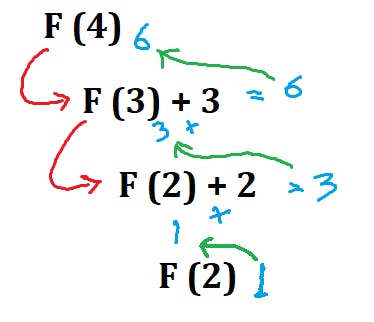
Hal pengulangan fungsi yang terus-menerus inilah yang dapat menyebabkan membengkaknya kebutuhan memori seiring dengan jumlah data (dalam hal ini jumlah orang) yang harus diproses.
Barisan aritmetika merupakan barisan bilangan yang mempunyai beda (selisih) yang tetap di antara suku-sukunya yang saling berdekatan, sedangkan deret aritmetika merupakan jumlah suku ke- n pertama pada barisan aritmetika 2.
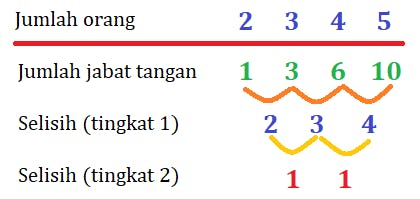
Jika melihat pada permasalahan menghitung jumlah jabat tangan ini, maka pendekatan yang lebih sesuai adalah pola barisan bilangan bertingkat, yaitu tingkat 2. Rumusnya adalah sebagai berikut.
Un = an2 + bn + c
Jadi, kalau diuraikan hingga tuntas, pola barisan yang diperoleh adalah sebagai berikut. Detail teori cara penurunan (atau penguraian) rumus sila merujuk ke laman web ini .
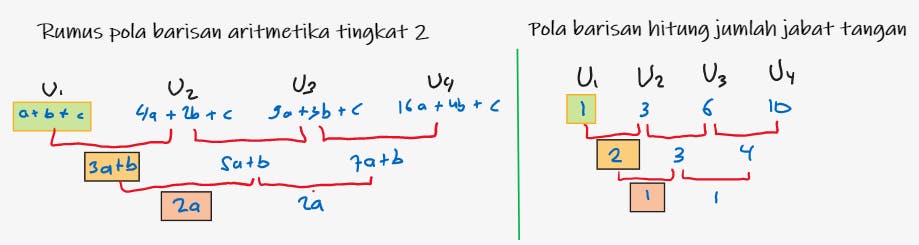
Setelah dilakukan substitusi, diperoleh nilai a=0.5, b=0.5, c=0. Sehingga, kalau dikembalikan ke rumus Un sebelumnya, dapat kita buat kodenya sebagai berikut.
def Barisan_Aritmetika_Tingkat_2(jml_orang):
n = jml_orang - 1
a, b, c = 0.5, 0.5, 0
Un = a*(n**2) + (b*n) + c
return Un
Nilai a, b, dan c harus selalu dihitung dan disesuaikan dengan pola baris soal yang kita miliki.
Untuk metode deret aritmetika ini mirip dengan penyelesaian pada metode rekursif, yaitu melihat pola penjumlahan yang menghasilkan jumlah jabat tangan.
2 orang = 1
3 orang = 3 = (1 + 2)
4 orang = 6 = (1 + 2 + 3)
5 orang =10 = (1 + 2 + 3 + 4)
...
n orang = (1 + 2 + 3 + … + (n – 1))
Dalam hal ini kita menggunakan rumus untuk menentukan jumlah bilangan pada suku ke- n.
Sn = n/2 . (a + Un)
di mana:
n = Un = n-1
a = suku pertama = 1
Sehingga, dapat dituliskan kodenya adalah sebagai berikut.
def Deret_Aritmetika(jml_orang):
n = jml_orang-1
return (n / 2) * (1 + n)
Rumus lain yang menghasilkan nilai yang sama adalah (jml_orang**2-jml_orang)/2.
Topik permutasi dan kombinasi dipelajari untuk menghitung peluang, dan sudah diajarkan untuk siswa kelas menengah atas. Teori lengkap dapat dibaca di laman web ini. Untuk menyelesaikan kasus menghitung jumlah jabat tangan, dikarenakan tidak diperlukan memperhatikan urutan siapa yang melakukan jabat tangan terlebih dahulu, maka kita akan selesaikan menggunakan metode kombinasi.
Rumus kombinasi:
C(n, r) = n!/(r! (n – r)!)
dimana:
C(n, r) : permutasi r objek dari n objek yang ada
n : banyaknya objek keseluruhan
r : banyaknya objek yang diamati/diberi perlakuan
Dalam kasus jabat tangan, n adalah jumlah orang, dan r adalah jumlah orang minimal terjadinya jabat tangan, yaitu 2 orang. Sehingga, untuk menghitung jumlah jabat tangan yang terjadi dalam 5 orang, persamaannya dapat kita tulis sebagai berikut.
C(5,2) = 5! / (5!x3!) = 10
Jika kita tuliskan ke bentuk kode:
from math import factorial
def Kombinasi_Salaman(jml_orang):
return factorial(jml_orang) / (factorial(jml_orang - 2) * factorial(2))
Fungsi factorial diimpor dari paket modul math bawaan Python, lebih efektif dibanding membuat fungsi faktorial sendiri walaupun memungkinkan.
Dari kelima metode ini, setelah diterapkan dalam bahasa pemrograman Python, penggunaan metode jenis penerapan rumus seperti baris dan deret aritmetika dipastikan lebih cepat dibandingkan metode lain. Hal ini disebabkan pemrosesan dilakukan hanya menghitung parameter masukan pada rumus yang diacu. Hanya saja, penentuan rumus harus dicari terlebih dahulu sebelum dapat diterapkan pada kode. Sedangkan metode selainnya, di dalamnya terdapat berbagai macam komputasi yang sering kali dilakukan perulangan lebih dari satu kali.
Namun dengan adanya perangkat modern saat ini, perbedaan waktu komputasi belum terlalu signifikan, hanya dalam satuan mikrodetik. Berikut ini contoh hasil pengujian waktu komputasi dengan nilai jumlah orang 2000, jumlah pengujian masing-masing metode 10 kali, yang menghasilkan jumlah jabat tangan: 1999000.
Metode 1 - Iterative
Waktu: [176.5 162.4 155.3 207.9 141.8 158.1 161. 160.5 158.7 160.3] mikrodetik
Max: 207.9, Min: 141.8, Avg: 164.25Metode 2 - Rekursif
Waktu: [1885.1 651.5 613.2 609.7 826.7 623. 610.9 605.8 607.5 587.1] mikrodetik
Max: 1885.1, Min: 587.1, Avg: 762.05Metode 3 - Barisan Aritmetika Bertingkat Dua
Waktu: [4.7 1.3 1.1 0.9 0.9 0.9 0.8 0.8 0.9 0.9] mikrodetik
Max: 4.7, Min: 0.8, Avg: 1.32Metode 4 - Deret Aritmetika (Jumlah Suku)
Waktu: [2.1 1. 0.7 0.7 0.7 0.8 0.7 0.7 0.7 0.8] mikrodetik
Max: 2.1, Min: 0.7, Avg: 0.89Metode 5 - Kombinasi (Faktorial)
Waktu: [518.1 495.1 488.5 489.5 485.8 487.5 487.7 488.4 447.2 356.8] mikrodetik
Max: 518.1, Min: 356.8, Avg: 474.46000000000004Waktu tercepat: 0.700 mikrodetik, Metode: Deret Aritmetika.
Waktu tercepat rata-rata: 0.890 mikrodetik, Metode: Deret Aritmetika.
Dan grafiknya adalah sebagai berikut.
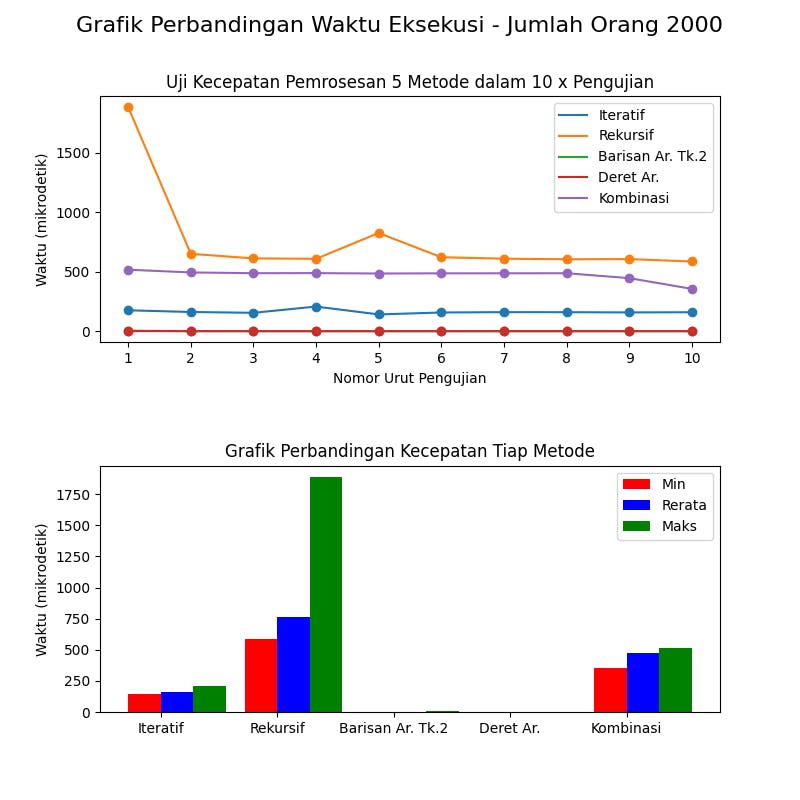
Demikian tutorial menyelesaikan kasus menghitung jumlah jabat tangan dari sejumlah orang menggunakan 5 metode berbeda dalam Python. Semoga bermanfaat.
Terima Kasih.
Kode sumber lengkap tersedia di repo github.
Demo online.